Optimize Bigram based on Yoshua et.'s paper

Link

Paper Link

Brief Description

Introducing embedding word to solve the problem of matrix being too sparse

• Tranditional NLP: using one_hot dog -> [1, 0, 0, 0, 0]
• Embedding word: Take the corresponding word vector from a shared parameter matrix C
  • dog - > [1.324, 2.23, 4.234]
• PS: In this section, same logic in bigrams mapping

Note

• Overview
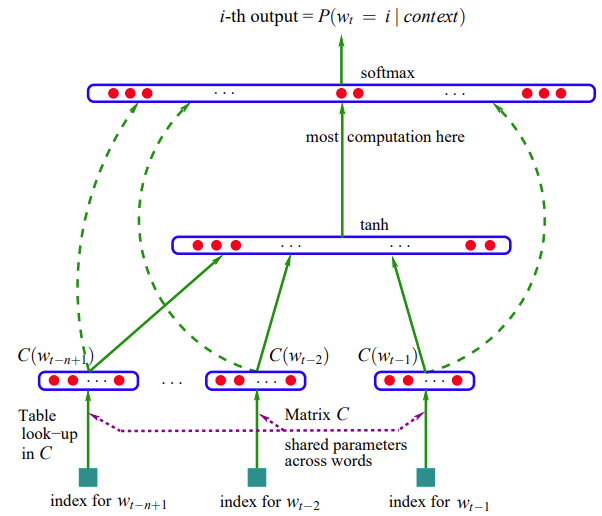
  • The model is designed for predicting the probability of a word sequence.
  • Uses one-hot encoding for input word representation.
  • Applies a hidden layer with activation (e.g., tanh).
  • Uses softmax to normalize output probabilities (ensuring they sum to 1).
• Encoding and Table Mapping C Table: A lookup table that maps input sequences to specific values. -CX → C[X] is used to convert a 2D table (C) into 3D representations.
  • Example:
    • C[X][1][2] maps to a stored value.
    • C[X][1][2]=C[1], meaning indexing refers to specific stored values.
• Overfitting or Underfitting
  • If training accuracy is high but validation accuracy is low, overfitting might be happening
  • Parameter Tuning
    • Optimize learning rate (draw the pic)
    • Adjust batch size(big size for stabilize training, small size for improve generalization)
    • Tune hidden layer sizes to balance model complexity and performance.
• Torch
  • cross_entropy same as the last one

    # cross_entropy equals
    probs = counts / counts.sum(1, keepdim=True)
    loss = -probs[torch.arange(len(xs)), ys].log().mean() + 0.01*(W**2).mean()
    loss
    

  • Scalar: only number
  • Tensor: n-dim array
  • When to use scalars and when to use tensors?
    • Scalars: loss, autograd, mathematical operations
    • Tensors: Input to the neural network (batch data) or matrix operation

Code

Pre-setting

import random

words = open('names.txt', 'r').read().splitlines()

chars=sorted(list(set(''.join(words))))
stoi = {s:i+1 for i,s in enumerate(chars)}
stoi['.'] = 0
itos = {i:s for s,i in stoi.items()}

# context length: how many characters do we take to predict the next one?
# slide window
block_size = 3 

# Calculate to make dataset respectively
def build_dataset(words):  
    X, Y = [], []
    for w in words:
        #print(w)
        context = [0] * block_size
        for ch in w + '.':
            ix = stoi[ch]
            X.append(context)
            Y.append(ix)
            context = context[1:] + [ix] 
        
    X = torch.tensor(X)
    Y = torch.tensor(Y)
    return X, Y
random.seed(1337)
random.shuffle(words)
n = len(words)
n1 = int(0.8 * n)
n2 = int(0.9 * n)

# Training data | validation data | test data
Xtr, Ytr = build_dataset(words[:n1])
Xdev, Ydev = build_dataset(words[n1:n2])
Xte, Yte = build_dataset(words[n2:])

g = torch.Generator().manual_seed(2147483647) 
# Means each block has 10 dim -> [lens(X), 10]
C = torch.randn((27, 10), generator=g)

# Input layer to hidden layer(tanh)
W1 = torch.randn((30, 200), generator=g)
b1 = torch.randn(200, generator=g)
# Hidden layer to output layer
W2 = torch.randn((200, 27), generator=g)
b2 = torch.randn(27, generator=g)
parameters = [C, W1, b1, W2, b2]

# in this case: 30*200(W1) + 200(b1) + 200*27(W2) + 27(b2) + 27*10(C)
sum(p.nelement() for p in parameters) 

for p in parameters:
    p.requires_grad = True

# Help us the know the best learning rate
lre = torch.linspace(-3, 0, 1000)
lrs = 10**lre
lri = []
lossi = []
stepi = []

Training procedure

for i in range(200000):
    # minibatch construct to reduce time
    # returns a tensor of random indices of size 32
    # for each indice, the range (0, Xtr.shape[0]) = (0, 1537)
    ix = torch.randint(0, Xtr.shape[0], (32,))
    
    # forward pass(training data only)
    emb = C[Xtr[ix]] # (32, 3, 10)
    
    h = torch.tanh(emb.view(-1, 30) @ W1 + b1) # (32, 200)
    logits = h @ W2 + b2 # (32, 27)
    loss = F.cross_entropy(logits, Ytr[ix])
    #print(loss.item())
    
    # backward pass
    for p in parameters:
    # avoid accumulating gradients
        p.grad = None
    loss.backward()
    
    # update
    lr = 0.1 if i < 100000 else 0.01
    for p in parameters:
        p.data += -lr * p.grad

    # track stats
    stepi.append(i)
    lossi.append(loss.log10().item())

Samples

# sample from the model
g = torch.Generator().manual_seed(2147483647 + 10)

for _ in range(20):
    
    out = []
    context = [0] * block_size # initialize with all ...
    while True:
        emb = C[torch.tensor([context])] # (1,block_size,d)
        h = torch.tanh(emb.view(1, -1) @ W1 + b1)
        logits = h @ W2 + b2
        probs = F.softmax(logits, dim=1)
        ix = torch.multinomial(probs, num_samples=1, generator=g).item()
        context = context[1:] + [ix]
        out.append(ix)
        if ix == 0:
            break
    
    print(''.join(itos[i] for i in out))

More details about word embedding